Vadazoeca: Complex number

A complex number is a number consisting of a real and imaginary part. It can be written in the form a + bi, where a and b are real numbers, and i is the standard imaginary unit with the property i ² = −1. The complex numbers contain the ordinary real numbers, but extend them by adding in extra numbers and correspondingly expanding the understanding of addition and multiplication.

Complex numbers were first conceived and defined by the Italian mathematician Gerolamo Cardano, who called them "fictitious", during his attempts to find solutions to cubic equations. The solution of a general cubic equation in radicals (without trigonometric functions) may require intermediate calculations containing the square roots of negative numbers, even when the final solutions are real numbers, a situation known as casus irreducibilis. This ultimately led to the fundamental theorem of algebra, which shows that with complex numbers, a solution exists to every polynomial equation of degree one or higher. Complex numbers thus form an algebraically closed field, where any polynomial equation has a root.
The rules for addition, subtraction, multiplication, and division of complex numbers were developed by the Italian mathematician Rafael Bombelli. A more abstract formalism for the complex numbers was further developed by the Irish mathematician William Rowan Hamilton, who extended this abstraction to the theory of quaternions.
Complex numbers are used in a number of fields, including: engineering, electromagnetism, quantum physics, applied mathematics, and chaos theory. When the underlying field of numbers for a mathematical construct is the field of complex numbers, the name usually reflects that fact. Examples are complex analysis, complex matrix, complex polynomial, and complex Lie algebra.
Complex numbers are plotted on the complex plane, on which the real part is on the horizontal axis, and the imaginary part on the vertical axis.

A complex number can be visually represented as a pair of numbers forming a vector on a diagram called an Argand diagram, representing the complex plane.

Introduction and definition

Complex numbers have been introduced to allow for solutions of certain equations that have no real solution: the equation

$x^2 + 1 = 0 \,$

has no real solution x, since the square of x is 0 or positive, so x² + 1 cannot be zero. Complex numbers are a solution to this dilemma. The idea is to enhance the real numbers by adding a number i whose square is −1, so that x = i and x = -i are the two solutions to the preceding equation.

Definition

A complex number is an expression of the form

$a+bi \ .$

Here a and b are real numbers, and i is a mathematical symbol which is called imaginary unit. For example, -3.5 + 2i is a complex number.
The real number a of the complex number z = a + bi is called the real part of z and the real number b is the imaginary part. They are denoted Re(z) or ℜ(z) and Im(z) or ℑ(z), respectively. For example,

$\operatorname{Re}(-3.5 + 2i) = -3.5 \$

$\operatorname{Im}(-3.5 + 2i) = 2 \$

Some authors write a+ib instead of a+bi. In some disciplines (in particular, electrical engineering, where i is a symbol for current), the imaginary unit i is instead written as j, so complex numbers are written as a + bj or a + jb.
A real number is thus a special case of a complex number: every real number a can be regarded as a complex number with an imaginary part of zero, that is to say, a + 0i. Complex numbers whose real part is zero, that is to say, those of the form 0 + bi, are called imaginary numbers. It is common to write a for a + 0i and bi for 0 + bi. Moreover, when b is negative, it is common to write a − (−b)i instead of a + bi, for example 3 − 4i instead of 3 + (−4)i.
The set of all complex numbers is denoted by C or $\mathbb{C}$ .

Addition and subtraction

Complex numbers are added by adding the real and imaginary parts of the summands. That is to say:

$(a+bi) + (c+di) = (a+c) + (b+d)i. \$

Similarly, subtraction is defined by

$(a+bi) - (c+di) = (a-c) + (b-d)i.\$

Using the visualization of complex numbers in the complex plane, the addition has the following geometric interpretation: the sum of two complex numbers A and B, interpreted as points of the complex plane, is the point X obtained by building a parallelogram three of whose vertices are 0, A and B. Equivalently, X is the point such that the triangles with vertices 0, A, B, and X, B, A, are congruent.

Multiplication and division

The multiplication of two complex numbers is defined by the following formula: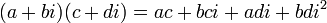

$(a+bi) (c+di) = (ac-bd) + (bc+ad)i.\$

In particular, the square of the imaginary unit is −1:

$i^2 = ii = -1.\$

The preceding definition of multiplication of general complex numbers is the natural way of extending this fundamental property of the imaginary unit. Indeed, treating i as a variable, the formula follows from this

$(a+bi) (c+di) = ac + bci + adi + bdi^2 \$ (distributive law)

$= ac + bidi + bci + adi \$ (commutative law of addition—the order of the summands can be changed)

$= ac + bdi^2 + (bc+ad)i \$ (commutative law of multiplication—the order of the factors can be changed

$= (ac-bd) + (bc + ad)i \$ (fundamental property of the imaginary unit).

The division of two complex numbers is defined by the following formula:

$\,\frac{a + bi}{c + di} = \left({ac + bd \over c^2 + d^2}\right) + \left( {bc - ad \over c^2 + d^2} \right)i,$

The real and imaginary part (c and d, respectively) of the denominator must not both be zero for the division to be defined. Division is defined in this way in order because the product of the right hand expression with c + di (using the previous formula for multiplication) is a + bi. Thus, dividing a + bi by c + di and then multiplying it with c + di again gives back a + bi, as is familiar from real or rational numbers.

Square root

The square roots of a + bi (with b ≠ 0) are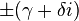 $\pm (\gamma + \delta i)$ , where

$\gamma = \sqrt{\frac{a + \sqrt{a^2 + b^2}}{2}}$

and

$\delta = \frac{|b|}{b} \sqrt{\frac{-a + \sqrt{a^2 + b^2}}{2}}.$

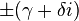This can be seen by squaring $\pm (\gamma + \delta i)$ to obtain a + bi. Here 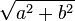$\sqrt{a^2 + b^2}$ is called the modulus of a + bi, and the square root with non-negative real part is called the principal square root.

Conjugation

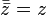The complex conjugate of the complex number z = x + yi is defined to be x − yi. It is denoted $\bar{z}$ or $z^*\,$ . Geometrically, $\bar{z}$ is the "reflection" of z about the real axis. In particular, conjugating twice gives the original complex number: $\bar{\bar{z}}=z$ .
The real and imaginary parts of a complex number can be extracted using the conjugate:

$\operatorname{Re}\,(z) = \tfrac{1}{2}(z+\bar{z}), \,$

$\operatorname{Im}\,(z) = \tfrac{1}{2i}(z-\bar{z}). \,$

Moreover, a complex number is real if and only if it equals its conjugate.
Conjugation distributes over the standard arithmetic operations:

$\overline{z+w} = \bar{z} + \bar{w}, \,$

$\overline{z w} = \bar{z} \bar{w}, \,$

$\overline{(z/w)} = \bar{z}/\bar{w} \,$

The reciprocal of a nonzero complex number z = x + yi is given by

$\frac{1}{z}=\frac{\bar{z}}{z \bar{z}}=\frac{\bar{z}}{x^2+y^2}.$

This formula can be used to compute the multiplicative inverse of a complex number if it is given in rectangular coordinates. Inversive geometry, a branch of geometry studying more general reflections than ones about a line, can be expressed in terms of complex numbers, too.

Polar form

Absolute value and argument

Another way of encoding points in the complex plane than using the x- and y-coordinates is to use the distance of a point P to O, the point whose coordinates are (0, 0) (origin), and the angle of the line through P and O. This idea leads to the polar form of complex numbers.
The absolute value (or modulus or magnitude) of a complex number z = x+yi is

$\textstyle r=|z|=\sqrt{x^2+y^2}.\,$

If z is a real number (i.e., y = 0), then r = |x|. In general, by Pythagoras' theorem, r is the distance of the point P representing the complex number z to the origin.
The argument or phase of z is the angle to the real axis, and is written as

arg(z)

. As with the modulus, the argument can be found from the rectangular form

x + i y

$\varphi = \arg(z) = \begin{cases} \arctan(\frac{y}{x}) & \mbox{if } x > 0 \\ \arctan(\frac{y}{x}) + \pi & \mbox{if } x < 0 \mbox{ and } y \ge 0\\ \arctan(\frac{y}{x}) - \pi & \mbox{if } x < 0 \mbox{ and } y < 0\\ \frac{\pi}{2} & \mbox{if } x = 0 \mbox{ and } y > 0\\ -\frac{\pi}{2} & \mbox{if } x = 0 \mbox{ and } y < 0\\ \mbox{undefined } & \mbox{if } x = 0 \mbox{ and } y = 0 \end{cases}$

The value of φ can change by any multiple of 2π and still give the same angle (note that radians are being used). Hence, the arg function is sometimes considered as multivalued. Normally, as given above, the principal value in the interval

( - π,π]

is chosen. Values in the range

[0,2π)

are obtained by adding

2π

if the value is negative. The polar angle of the origin is undefined but the value 0 is commonly used.
Together, r and φ give another way of representing complex numbers, the polar form, as the combination of modulus and argument fully specify the position of a point on the plane. Recovering the original rectangular co-ordinates from the polar form is done by the formula called trigonometric form

$z = r(\cos \varphi + i\sin \varphi ).\,$

Using Euler's formula this can be written as

$z = r e^{i \varphi}.$

Using the cis function, this is sometimes abbreviated to

$z = r \ \operatorname{cis} \ \varphi. \,$

In angle notation, often used in electronics to represent a phasor with amplitude r and phase φ it is written as

$z = r \ang \varphi . \,$

Figure 2: The argument φ and modulus r locate a point on an Argand diagram;

r (cosφ + i sinφ)

r e i φ

are polar expressions of the point.

Multiplication, division and exponentiation in polar form

The relevance of representing complex numbers in polar form stems from the fact that the formulas for multiplication, division and exponentiation are simpler than the ones using Cartesian coordinates. Given two complex numbers z₁ = r₁(cos φ₁ + isin φ₁) and z₂ =r₂(cos φ₂ + isin φ₂) the formula for multiplication is

$z_1 z_2 = r_1 r_2 (\cos(\varphi_1 + \varphi_2) + i \sin(\varphi_1 + \varphi_2)).$

In other words, the absolute values are multiplied and the arguments are added to yield the polar form of the product. For example, multiplying by i corresponds to a quarter-rotation counter-clockwise, which gives back i² = −1. The picture at the right illustrates the multiplication of

$(2+i)(3+i)=5+5i \,$

Since the real and imaginary part of 5+5i are equal, the argument of that number is 45 degrees, or π/4 (in radian). On the other hand, it is also the sum of the angles at the origin of the red and blue triangle are arctan(1/3) and arctan(1/2), respectively. Thus, the formula

$\frac{\pi}{4} = \arctan\frac{1}{2} + \arctan\frac{1}{3}$

holds. As the arctan function can be approximated highly efficiently, formulas like this—known as Machin-like formulas—are used for high-precision approximations of π.
Similarly, division is given by

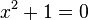
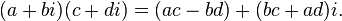
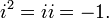
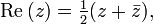
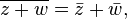
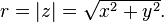
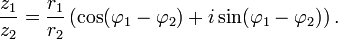
$\frac{z_1}{ z_2} = \frac{r_1}{ r_2} \left(\cos(\varphi_1 - \varphi_2) + i \sin(\varphi_1 - \varphi_2)\right).$

This also implies de Moivre's formula for exponentiation of complex numbers with integer exponents:

$z^n = r^n\,(\cos n\varphi + i \sin n \varphi).$

The n-th roots of z are given by

$\sqrt[n]{z} = \sqrt[n]r \left( \cos \left(\frac{\varphi+2k\pi}{n}\right) + i \sin \left(\frac{\varphi+2k\pi}{n}\right)\right)$

for any integer k satisfying 0 ≤ k ≤ n − 1. Here $\sqrt[n]{r}$ is the usual (positive) nth root of the positive real number r. While the nth root of a positive real number r is chosen to be the positive real number c satisfying cⁿ = x there is no natural way of distinguishing one particular complex nth root of a complex number. Therefore, the nth root of z is considered as a multivalued function (in z), as opposed to a usual function f, for which f(z) is a uniquely defined number. Formulas such as

$\sqrt[n]{z^n} = z$