Newton's laws of motion consist of three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motiondue to those forces. They have been expressed in several different ways over nearly three centuries, and can be summarized as follows:
- First law: Every body remains in a state of rest or uniform motion (constant velocity) unless it is acted upon by an external unbalanced force. This means that in the absence of a non-zero net force, the center of mass of a body either remains at rest, or moves at a constant speed in a straight line.
- Second law: A body of mass m subject to a force F undergoes an acceleration a that has the same direction as the force and a magnitude that is directly proportional to the force and inversely proportional to the mass, i.e., F = ma. Alternatively, the total force applied on a body is equal to the time derivative of linear momentum of the body.
- Third law: The mutual forces of action and reaction between two bodies are equal, opposite and collinear. This means that whenever a first body exerts a force F on a second body, the second body exerts a force −F on the first body. F and −F are equal in magnitude and opposite in direction. This law is sometimes referred to as the action-reaction law, with F called the "action" and −F the "reaction". The action and the reaction are simultaneous.
The three laws of motion were first compiled by Sir Isaac Newton in his work Philosophiæ Naturalis Principia Mathematica, first published on July 5, 1687. Newton used them to explain and investigate the motion of many physical objects and systems. For example, in the third volume of the text, Newton showed that these laws of motion, combined with his law of universal gravitation, explained Kepler's laws of planetary motion.
Newton's laws are applied to bodies (objects) which are considered or idealized as a particle, in the sense that the extent of the body is neglected in the evaluation of its motion, i.e., the object is small compared to the distances involved in the analysis, or the deformation and rotation of the body is of no importance in the analysis. Therefore, a planet can be idealized as a particle for analysis of its orbital motion around a star.
In their original form, Newton's laws of motion are not adequate to characterize the motion of rigid bodies and deformable bodies. Leonard Euler in 1750 introduced a generalization of Newton's laws of motion for rigid bodies called the Euler's laws of motion, later applied as well for deformable bodies assumed as a continuum. If a body is represented as an assemblage of discrete particles, each governed by Newton’s laws of motion, then Euler’s laws can be derived from Newton’s laws. Euler’s laws can, however, be taken as axioms describing the laws of motion for extended bodies, independently of any particle structure.
Newton's Laws hold only with respect to a certain set of frames of reference called Newtonian or inertial reference frames. Some authors interpret the first law as defining what an inertial reference frame is; from this point of view, the second law only holds when the observation is made from an inertial reference frame, and therefore the first law cannot be proved as a special case of the second. Other authors do treat the first law as a corollary of the second. The explicit concept of an inertial frame of reference was not developed until long after Newton's death.
In the given interpretation mass, acceleration, momentum, and (most importantly) force are assumed to be externally defined quantities. This is the most common, but not the only interpretation: one can consider the laws to be a definition of these quantities.
At speeds approaching the speed of light the effects of special relativity must be taken into account.
Newton's second law
The second law states that the net force on a particle is equal to the time rate of change of its linear momentum p in an inertial reference frame:
where, since the law is valid only for constant-mass systems, the mass can be taken outside the differentiation operator by the constant factor rule in differentiation. Thus,
where F is the net force applied, m is the mass of the body, and a is the body's acceleration. Thus, the net force applied to a body produces a proportional acceleration.
Any mass that is gained or lost by the system will cause a change in momentum that is not the result of an external force. A different equation is necessary for variable-mass systems (see below).
Consistent with the first law, the time derivative of the momentum is non-zero when the momentum changes direction, even if there is no change in its magnitude; such is the case with uniform circular motion. The relationship also implies the conservation of momentum: when the net force on the body is zero, the momentum of the body is constant. Any net force is equal to the rate of change of the momentum.
Newton's second law requires modification if the effects of special relativity are to be taken into account, because at high speeds the approximation that momentum is the product of rest mass and velocity is not accurate.
Impulse
Since force is the time derivative of momentum, it follows that
Variable-mass systems
Variable-mass systems, like a rocket burning fuel and ejecting spent gases, are not closed and cannot be directly treated by making mass a function of time in the second law. The reasoning, given in An Introduction to Mechanics by Kleppner and Kolenkow and other modern texts, is that Newton's second law applies fundamentally to particles. In classical mechanics, particles by definition have constant mass. In case of a well-defined system of particles, Newton's law can be extended by summing over all the particles in the system:
where Fnet is the total external force on the system, M is the total mass of the system, and acm is the acceleration of the center of mass of the system.
Variable-mass systems like a rocket or a leaking bucket cannot usually be treated as a system of particles, and thus Newton's second law cannot be applied directly. Instead, the general equation of motion for a body whose mass m varies with time by either ejecting or accreting mass is obtained by rearranging the second law and adding a term to account for the momentum carried by mass entering or leaving the system:
where u is the relative velocity of the escaping or incoming mass with respect to the center of mass of the body. Under some conventions, the quantity u dm/dt on the left-hand side, known as the thrust, is defined as a force (the force exerted on the body by the changing mass, such as rocket exhaust) and is included in the quantity F. Then, by substituting the definition of acceleration, the equation becomes
References: wikipedia.com




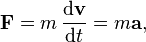


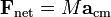

















0 comments:
Post a Comment