Trigonometry (from Greek trigōnon "triangle" + metron "measure" or from Sanskrit trikon "triangle" + miti "measurement" = trikonmiti) is a branch of mathematics that studies triangles and the relationships between their sides and the angles between sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves. The field evolved during the third century BC as a branch of geometry used extensively for astronomical studies.
Trigonometry is usually taught in middle and secondary schools either as a separate course or as part of a precalculus curriculum. It has applications in both pure mathematics and applied mathematics, where it is essential in many branches of science and technology. A branch of trigonometry, called spherical trigonometry, studies triangles on spheres, and is important in astronomy and navigation.
Applications of trigonometry
There are an enormous number of uses of trigonometry and trigonometric functions. For instance, the technique of triangulation is used in astronomy to measure the distance to nearby stars, in geography to measure distances between landmarks, and in satellite navigation systems. The sine and cosine functions are fundamental to the theory of periodic functions such as those that describe sound and light waves.
Fields that use trigonometry or trigonometric functions include astronomy (especially for locating apparent positions of celestial objects, in which spherical trigonometry is essential) and hence navigation (on the oceans, in aircraft, and in space), music theory, acoustics, optics, analysis of financial markets, electronics, probability theory, statistics, biology, medical imaging (CAT scans and ultrasound), pharmacy, chemistry, number theory (and hence cryptology), seismology, meteorology, oceanography, many physical sciences, land surveying and geodesy, architecture, phonetics, economics, electrical engineering, mechanical engineering, civil engineering, computer graphics, cartography, crystallography and game development.
Standard Identities
Identities are those equations that hold true for any value.
1.:sin2A + cos2A = 1
2.:sec2A − tan2A = 1
3.:cosec2A − cot2A = 1
Angle Transformation Formulas
1.:sin(A + B) = sinA * cosB + cosA * sinB
2.:cos(A + B) = cosA * cosB − sinA * sinB
3.:sin(A − B) = sinA * cosB − cosA * sinB
4.:cos(A − B) = cosA * cosB + sinA * sinB
Common formulas
 |
| Triangle with sides a,b,c and respectively opposite angles A,B,C |
Certain equations involving trigonometric functions are true for all angles and are known as trigonometric identities. Some identities equate an expression to a different expression involving the same angles. These are listed in List of trigonometric identities. Triangle identities that relate the sides and angles of a given triangle are listed below.
In the following identities, A, B and C are the angles of a triangle and a, b and c are the lengths of sides of the triangle opposite the respective angles.
Law of sines
The law of sines (also known as the "sine rule") for an arbitrary triangle states:
where R is the radius of the circumscribed circle of the triangle:
Another law involving sines can be used to calculate the area of a triangle. Given two sides and the angle between the sides, the area of the triangle is:
Law of cosines
 |
| All of the trigonometric functions of an angle θ can be constructed geometrically in terms of a unit circle centered at O. |
The law of cosines (known as the cosine formula, or the "cos rule") is an extension of the Pythagorean theorem to arbitrary triangles:
or equivalently:
Law of tangents
The law of tangents:
Euler's formula
Euler's formula, which states that eix = cosx + isinx, produces the following analytical identities for sine, cosine, and tangent in terms of e and the imaginary unit i:

- References : wikipedia.com



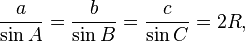
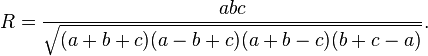
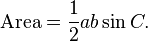
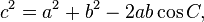

![\frac{a-b}{a+b}=\frac{\tan\left[\tfrac{1}{2}(A-B)\right]}{\tan\left[\tfrac{1}{2}(A+B)\right]}](http://upload.wikimedia.org/math/c/b/5/cb5c755b587d4e4e1f4367c492c4de8d.png)















0 comments:
Post a Comment