A capacitor (formerly known as condenser) is a passive electronic component consisting of a pair of conductors separated by a dielectric (insulator). When there is a potential difference (voltage) across the conductors, a static electric field develops in the dielectric that stores energy and produces a mechanical force between the conductors. An ideal capacitor is characterized by a single constant value, capacitance, measured in farads. This is the ratio of the electric charge on each conductor to the potential difference between them.
Capacitors are widely used in electronic circuits for blocking direct current while allowing alternating current to pass, in filter networks, for smoothing the output of power supplies, in the resonant circuits that tune radios to particular frequencies and for many other purposes.
The effect is greatest when there is a narrow separation between large areas of conductor, hence capacitor conductors are often called "plates", referring to an early means of construction. In practice the dielectric between the plates passes a small amount of leakage current and also has an electric field strength limit, resulting in a breakdown voltage, while the conductors and leads introduce an undesired inductance and resistance.
A capacitor consists of two conductors separated by a non-conductive region called the dielectric medium though it may be a vacuum or a semiconductor depletion region chemically identical to the conductors. A capacitor is assumed to be self-contained and isolated, with no net electric charge and no influence from any external electric field. The conductors thus hold equal and opposite charges on their facing surfaces, and the dielectric develops an electric field. In SI units, a capacitance of one farad means that one coulomb of charge on each conductor causes a voltage of one volt across the device.
The capacitor is a reasonably general model for electric fields within electric circuits. An ideal capacitor is wholly characterized by a constant capacitance C, defined as the ratio of charge ±Q on each conductor to the voltage V between them:
The effect is greatest when there is a narrow separation between large areas of conductor, hence capacitor conductors are often called "plates", referring to an early means of construction. In practice the dielectric between the plates passes a small amount of leakage current and also has an electric field strength limit, resulting in a breakdown voltage, while the conductors and leads introduce an undesired inductance and resistance.
A capacitor consists of two conductors separated by a non-conductive region called the dielectric medium though it may be a vacuum or a semiconductor depletion region chemically identical to the conductors. A capacitor is assumed to be self-contained and isolated, with no net electric charge and no influence from any external electric field. The conductors thus hold equal and opposite charges on their facing surfaces, and the dielectric develops an electric field. In SI units, a capacitance of one farad means that one coulomb of charge on each conductor causes a voltage of one volt across the device.
The capacitor is a reasonably general model for electric fields within electric circuits. An ideal capacitor is wholly characterized by a constant capacitance C, defined as the ratio of charge ±Q on each conductor to the voltage V between them:
Energy storage
Work must be done by an external influence to "move" charge between the conductors in a capacitor. When the external influence is removed the charge separation persists in the electric field and energy is stored to be released when the charge is allowed to return to its equilibrium position. The work done in establishing the electric field, and hence the amount of energy stored, is given by:Current-voltage relation
The current i(t) through any component in an electric circuit is defined as the rate of flow of a charge q(t) passing through it, but actual charges, electrons, cannot pass through the dielectric layer of a capacitor, rather an electron accumulates on the negative plate for each one that leaves the positive plate, resulting in an electron depletion and consequent positive charge on one electrode that is equal and opposite to the accumulated negative charge on the other. Thus the charge on the electrodes is equal to the integral of the current as well as proportional to the voltage as discussed above. As with any antiderivative, a constant of integration is added to represent the initial voltage v (t0). This is the integral form of the capacitor equation, .
.
 .
.
DC circuits
A series circuit containing only a resistor, a capacitor, a switch and a constant DC source of voltage V0 is known as a charging circuit.[14] If the capacitor is initially uncharged while the switch is open, and the switch is closed at t = 0, it follows from Kirchhoff's voltage law that
Taking the derivative and multiplying by C, gives a first-order differential equation,
At t = 0, the voltage across the capacitor is zero and the voltage across the resistor is V0. The initial current is then i (0) =V0 /R. With this assumption, the differential equation yields
where τ0 = RC is the time constant of the system.
As the capacitor reaches equilibrium with the source voltage, the voltage across the resistor and the current through the entire circuit decay exponentially. The case of discharging a charged capacitor likewise demonstrates exponential decay, but with the initial capacitor voltage replacing V0 and the final voltage being zero.
AC circuits
Impedance, the vector sum of reactance and resistance, describes the phase difference and the ratio of amplitudes between sinusoidally varying voltage and sinusoidally varying current at a given frequency. Fourier analysis allows any signal to be constructed from a spectrum of frequencies, whence the circuit's reaction to the various frequencies may be found. The reactance and impedance of a capacitor are respectively
where j is the imaginary unit and ω is the angular velocity of the sinusoidal signal. The - j phase indicates that the AC voltage V = Z I lags the AC current by 90°: the positive current phase corresponds to increasing voltage as the capacitor charges; zero current corresponds to instantaneous constant voltage, etc.
Note that impedance decreases with increasing capacitance and increasing frequency. This implies that a higher-frequency signal or a larger capacitor results in a lower voltage amplitude per current amplitude—an AC "short circuit" or AC coupling. Conversely, for very low frequencies, the reactance will be high, so that a capacitor is nearly an open circuit in AC analysis—those frequencies have been "filtered out".
Capacitors are different from resistors and inductors in that the impedance is inversely proportional to the defining characteristic, i.e. capacitance.
Parallel plate model
The simplest capacitor consists of two parallel conductive plates separated by a dielectric with permittivity ε (such as air). The model may also be used to make qualitative predictions for other device geometries. The plates are considered to extend uniformly over an area A and a charge density ±ρ = ±Q/A exists on their surface. Assuming that the width of the plates is much greater than their separation d, the electric field near the centre of the device will be uniform with the magnitude E = ρ/ε. The voltage is defined as the line integral of the electric field between the plates .
.
Networks
- For capacitors in parallel
- Capacitors in a parallel configuration each have the same applied voltage. Their capacitances add up. Charge is apportioned among them by size. Using the schematic diagram to visualize parallel plates, it is apparent that each capacitor contributes to the total surface area.
- For capacitors in series
- Connected in series, the schematic diagram reveals that the separation distance, not the plate area, adds up. The capacitors each store instantaneous charge build-up equal to that of every other capacitor in the series. The total voltage difference from end to end is apportioned to each capacitor according to the inverse of its capacitance. The entire series acts as a capacitor smaller than any of its components.

- Capacitors are combined in series to achieve a higher working voltage, for example for smoothing a high voltage power supply. The voltage ratings, which are based on plate separation, add up. In such an application, several series connections may in turn be connected in parallel, forming a matrix. The goal is to maximize the energy storage utility of each capacitor without overloading it.
- Series connection is also used to adapt electrolytic capacitors for AC use.
Equivalent circuit
An ideal capacitor only stores and releases electrical energy, without dissipating any. In reality, all capacitors have imperfections within the capacitor's material that create resistance. This is specified as the equivalent series resistance or ESR of a component. This adds a real component to the impedance:
Similarly to ESR, the capacitor's leads add equivalent series inductance or ESL to the component. This is usually significant only at relatively high frequencies. As inductive reactance is positive and increases with frequency, above a certain frequency capacitance will be canceled by inductance. High-frequency engineering involves accounting for the inductance of all connections and components.
If the conductors are separated by a material with a small conductivity rather than a perfect dielectric, then a small leakage current flows directly between them. The capacitor therefore has a finite parallel resistance, and slowly discharges over time (time may vary greatly depending on the capacitor material and quality).






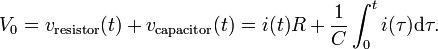

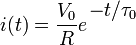


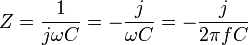
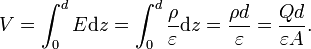
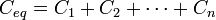















0 comments:
Post a Comment